Kernel Methods

Linear Algebra Terminologies

Relevantly, note that refers to the norm of the vector , where is it’s dimension.

The normalised vector is thus .

Thus, given column vectors: and , the norm is:

with the dot product of and , being:

Note that the dot product gives the similarity of two vectors:

• larger dot product indicates similarity
• smaller dot product indicates dissimilarity

Support Vector Machine Concepts

Summary

• Dual formulation of linear regression
• Kernel function as similarity functions
• Feature map Kernels

Linear Model

Weights can be rewritten as a linear combination of training data:

The linear model can then be rewritten:

Dual Formulation

This is the dual hypothesis , which contains a sum of dot products between all and , and parameters/weights .

Letting be a function defining a dot product:

we get:

The significance of k(u, v)

is a measure of similarity. Thus, we can replace it with other similarity functions.

Kernel Trick

Validity of kernel

For the kernel to be valid, it must be continuous symmetric positive-definite kenrel

With the transformed features, the new dual objective function looks like such:

There is no need to compute the transformation function explicitly.

With the kernel trick, we are then able to substitute the kernel in, allowing us to have SVM with infinite-dimensional features!

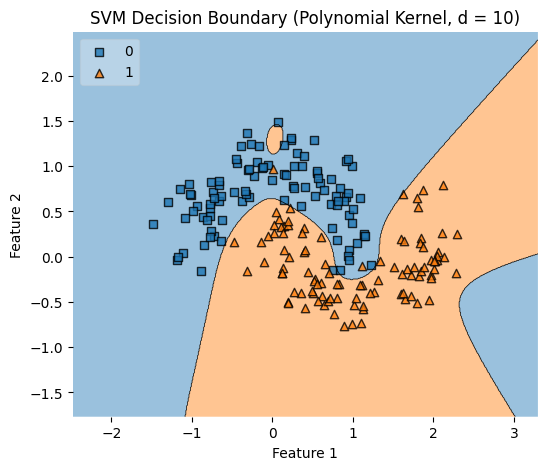
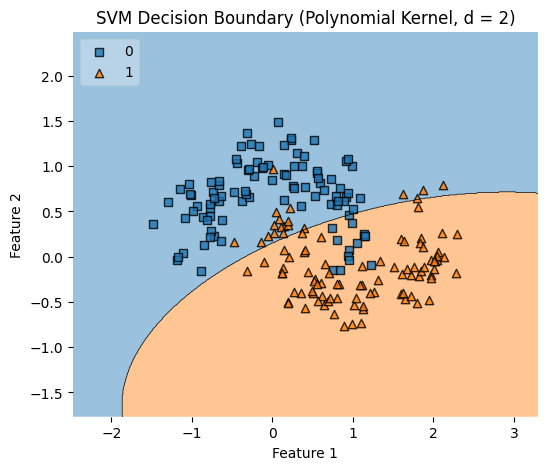
Polynomial Kernel

At the polynomial degree ,

At the polynomial degree 2,

Thus, we can generalise to degree , with terms:

Hyperparameters

The higher the degree ,

• the more complex the model is
• the higher the risk-of-overfitting
• the better the capturing of non-linear intricate relationships.

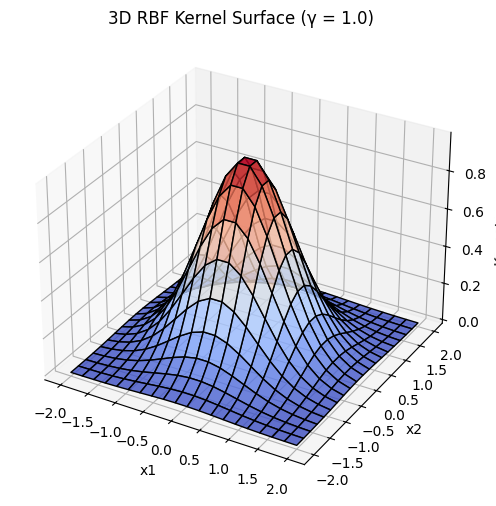
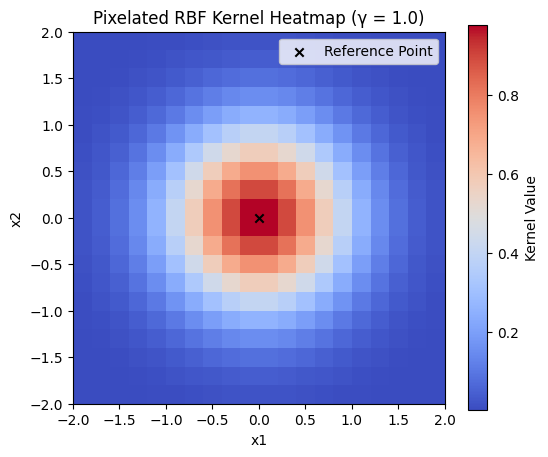
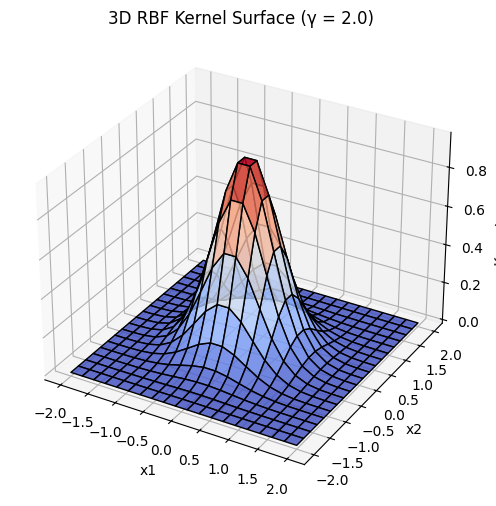
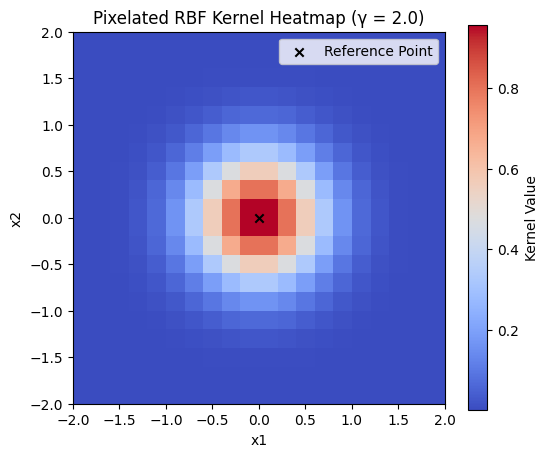
Gaussian Kernel (Radial Basis Function)

In this scenario, maps to infinite-dimensional features.

Hyperparameters

Let

Note that the surface becomes smaller as increases, meaning that as increases, the spread increases.

When is small (and is large):

• kernel function decays slowly, meaning points far from reference have high similarity
• smooth, globally connected decision boundaries
• good for simple patterns, may fail to capture fine details, higher risk of underfitting

When is large (and is small):

• kernel function decays quickly, meaning only close points have high similarity
• complex, decision boundaries
• good for capturing fine details, higher risk of overfitting

Feature Transformation

The most general case of a feature transformation is to take a dimensional feature vector and transform it into a dimensional feature vector:

Given

• input vector of dimension
• feature map of dimension , the hypothesis class is:

Dual Hypothesis with Transformed Features

Recall the dual hypothesis - with the feature mapping function :

Note that there is a dot product here, thus this can be generalised to:

Example

Given a non-linear decision boundary, for example:

In the first example, given the feature-transformation function , as the data is non-linearly separable, this fails the decision boundary.

However, using the function , where the new hypothesis:

However, can produce a huge number of features, making it not scalable.

Kernel Formation

Theorem (informal)

For any valid kernel , there exists a corresponding feature transformation .